Triangulation is a tactic used in chess endgames to put one´s opponent in zugzwang. It is normally used in king and pawn endgames when one king can maneuver on three adjacent squares in the shape of a triangle and maintain the basic position while the opposing king only has two such squares. Thus, if one king
triangulates by using three moves to return to the original square and the opposing king can´t do the same, he has lost a crucial tempo and gained the opposition (and see Chess strategy and tactics).
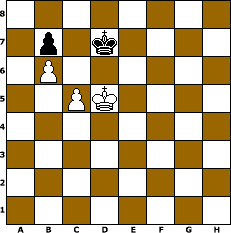
Consider this position, with white to move. Here, black has the opposition, and is keeping the white king out. However, if white had the opposition (i.e. it was black´s move in this position), the black king would have to move away from d7 and allow the white king to advance. Black´s king must stay close to where it is - he must prevent the c pawn from advancing and he must not let himself be driven to the edge of the board. When white´s king is on d5, black´s king must be on d7, with white to move. White has a triangle of squares available: d5, e5, and d4. White can win by the following maneuver, in algebraic notation:
1. Ke5 Kc6 (if 1... Ke7 then 2. c6 wins)
2. Kd4 Kd7
3. Kd5
and now the triangulation is complete and we have the same position but with black to move. There may follow:
3. ... Kc8
4. Ke6 Kd8
5. Kd6 Kc8
6. Ke7 Kb8
7. Kd7 Ka8
8. c6
and white will win. (There are other ways for white to win after his third move.)
|
