The Plachutta is a device found in chess problems: a white piece sacrifices itself on a square where it could be captured by one of two similarly-moving black pieces (for example, a bishop and a queen moving along a diagonal, or two rooks) moving along a different line; whichever black piece captures, it interferes with the other.
The Plachutta is related to a number of other problem themes: it can be regarded as a Wurzburg-Plachutta brought about by a white sacrifice on the critical square (a Wurzburg-Plachutta itself being a pair of Holzhausen interferences); or it can be thought of as a Novotny with similarly-moving (rather than differently-moving) black pieces involved (a Novotny itself being a Grimshaw brought about by a white sacrifice on the critical square). It can also be compared to the anti-Bristol, in which two similarly-moving black pieces interfere with each other along the same line.
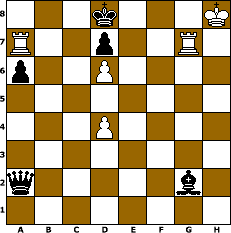
The problem to the right is a relatively simple example by William Shinkman, published in White Rooks, 1910. It is a mate in three (white moves first and must checkmate black in three moves against any defence). The key (first move of the solution; see chess problem terminology) is 1.d5 (see algebraic notation). Examining the initial position reveals why this works: white would like to play either 1.Ra8 or 1.Rg8, but the former is prevented by black´s bishop and the latter is prevented by black´s queen. 1.d5 blocks the paths of both black pieces to these squares, and whichever black piece takes the pawn interferes with the other and has to defend against both threats itself (to use chess jargon, it becomes overloaded). So, if 1...Qxd5 white can play 2.Ra8+ Qxa8, when the queen is deflected from her defence of g8, allowing 3.Rg8#, while if 1...Bxd5 white can play 2.Rg8+ Bxg8, deflecing the bishop from defence of a8, allowing 3.Ra8#.
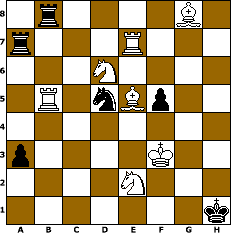
To the right is another relatively simple example, but this time it is two rooks, rather than bishop and queen, involved in the interferences. The problem, by D. J. Densmore, published in the Gazette-Times, 1916, is another mate in three. The key is 1.Nb7, which interferes with both rooks and so threatens both 2.Rh7# and 2.Rb1#. Black can defend with Raxb7, but this overloads the capturing rook, so white can play 2.Rb1+ Rxb1 3.Rh7#. The other capture is similar: 1...Rbxb7 2.Rh7+ Rxh7 3.Rb1#. Whichever rook captures, it interferes with the other and becomes overloaded, having to defend against two threats on its own.

Although the term Plachutta is confined to the world of chess problems, not being used in a wider chess context, the underlying Plachutta pattern does occasionally (though rarely) appear in an actual game. One example is to the right, a position which occurred in a 1914 game between Siegbert Tarrasch (with white) and an amateur (quoted in John Littlewood´s How to Play the Middle Game in Chess, Batsford, 1976). In the given position, the black queen defends against Qb7 and the rook on c8 defends against Rxc5. Tarrasch played 31.Bc7!, a Plachutta interference after which black cannot maintain control over both b7 and c5 (black actually resigned after this move). If 31...Rxc7 the rook is overloaded, having to look after both the key squares: 32.Qb7+ Rxb7 and the rook is deflected from defence of c5, allowing 33.Rxc5#. If instead 31...Qxc7 it is the queen which is overloaded: 32.Rxc5+ Qxc5 deflects the queen from defence of b7, allowing 33.Qb7+ Kxa5 34.Ra1#.
|
