A chess problem, formally called a chess composition, is a puzzle set by somebody using chess pieces on a chess board, presenting the solver with a particular task to be achieved. For instance, a position might be given with the instruction that white is to move first, and checkmate black in two moves against any possible defence. A person who creates such problems is known as a "composer". There is a good deal of specialised jargon used in chess problems; see chess problem terminology for a list.
Exactly what constitutes a chess problem is, to a degree, open to debate. However, the kinds of things published in the problem section of chess magazines, in specialist chess problem magazines, and in collections of chess problems in book form, tend to have certain common characteristics:
- The position is composed - that is, it has not been taken from an actual game, but has been invented for the specific purpose of providing a problem.
- There is a specific aim, for example, to checkmate black within a specified number of moves.
- There is a theme and the problem is aesthetically pleasing. A problem´s theme is an underlying idea, giving coherence and beauty to its solution.
Problems can be contrasted with tactical puzzles often found in chess columns or magazines in which the task is to find the best move or sequence of moves (usually leading to mate or gain of material) from a given position. Such puzzles are often taken from actual games, or at least have positions which look they could have arisen during a game, and are used for instructional purposes; problems, on the other hand, are invented positions, often with very "artificial" looking positions and solutions, not likely to arise in a game, and are appreciated more for their aesthetic than their instructional qualities.
Types of problem
There are various different types of chess problem:
- Directmates - white to move first and checkmate black within a specified number of moves against any defence. These are often referred to as "mate in n", where n is the number of moves within which mate must be delivered. In composing and solving competitions, directmates are further broken down into three classes:
- Two-movers - white to move and checkmate black in two moves against any defence
- Three-movers - white to move and checkmate black in no more than three moves against any defence
- More-movers - white to move and checkmate black in a given number of moves more than three against any defence
- Helpmates - black to move first cooperates with white to get his own king mated via legal moves
- Selfmates - white moves first and forces black to checkmate white´s king against black´s will
- Reflexmates - a selfmate in which each player must give mate if they are able to do so on their turn. When this stipulation applies only to black, it is a semi-reflexmate.
- Series-movers - one side makes a series of moves without reply to achieve a stipulated aim. Check may not be given except on the last move. A series-mover can be a:
- Series-mate - a directmate with white playing a series of moves without reply to checkmate black
- Series-helpmate - a helpmate in which black plays a series of moves without reply, and then white plays one move to checkmate black
- Series-selfmate - a selfmate in which white plays a series of moves leading to a position in which black is forced to give mate
- Series-reflexmate - a reflexmate in which white plays a series of moves leading to a position in which black can, and therefore must, give mate
All the above may also be found in forms of fairy chess - chess played with unorthodox rules, possibly using fairy pieces (unorthodox pieces).
In addition, there is the study, in which the stipulation is that white to play must win or draw. Almost all studies are endgame positions. Because the study is composed it is related to the problem, but because the stipulation is open-ended (the win or draw does not have to be achieved within any particular number of moves) it is usually thought of as separate from the problem. However, particularly long more-movers sometimes have the character of a study - there is no clear dividing line between the two.
In all the above types of problem, castling is assumed to be allowed unless it can be proved by retrograde analysis (see below) that the rook in question or king must have previously moved. En passant captures, on the other hand, are assumed not to be allowed, unless it can be proved that the pawn in question must have moved two squares on the previous move.
There are several other types of chess problem which do not follow the usual chess pattern of two sides playing moves towards checkmate. Some of these, like the knight´s tour are essentially one-offs, but other types have been revisited many times, with magazines, books and prizes being dedicated to them:
- Retrograde analysis - this is the act of working out from a given position, what previous move or moves have been played. A problem employing retrograde analysis may, for example, present a position and carry the stipulation "Find white´s last move" or "Has the bishop on c1 moved?". Problems such as these in which retrograde analysis is the main point are commonly called retros. Retrograde analysis may also have to be employed in more conventional problems (directmates and so on) to determine, for example, whether an en passant pawn capture or castling is possible. The most important sub-set of retro problems are:
- Shortest proof games - the solver must construct a game, starting from the normal initial position in chess, which ends with the position in a given diagram. The two sides cooperate to reach the position, but all moves must be legal. Usually the number of moves required to reach the position is given, though sometimes the task is simply to reach the given position in the shortest possible number of moves.
- Construction task - no diagram is given in construction tasks; instead the aim is to construct a game or position with certain features. For example, Sam Loyd devised the problem: "Construct a game which ends with black delivering discovered checkmate on move four" (published in Le Sphinx, 1866; the solution is 1.f3 e5 2.Kf2 h5 3.Kg3 h4+ 4.Kg4 d5#). Some construction tasks ask for a maximum or minimum number of something to be arranged, for example a game with the maximum possible number of consecutive discovered checks, or a position in which all sixteen pieces control the minimum number of squares.
Beauty in chess problems
There are no official standards by which to distinguish a beautiful problem from a poor one, and judgement varies from individual to individual as well as from generation to generation, but modern taste generally recognizes the following elements as being important if a problem is to be regarded as beautiful:
- The problem position must be legal. That is to say, the diagram must be reachable via a legal chess game which begins from the standard opening position. It is not considered a defect if the diagram can only be reached via a game containing gross blunders. Chess problems, on the whole, are not created for the purpose of practical chess training.
- The first move of the problem´s solution (the key move or key) must be unique. A problem which has two keys is said to be cooked, and would not be published in any magazine. An exception is problems which intentionally have more than one solution, which compliment or contrast each other in some way - this type of problem is particularly common in helpmates.
- Some would say that, ideally, there should only be one possible white move after every black move, although this is not nearly so important. A choice of white moves other than the first move is a dual. Duals are often excusable if the problem is strong in other regards.
- The solution should be explicable in terms of a theme or themes, rather than emerging from disjointed calculation. Many of the more common themes have been given names by problemists (see chess problem terminology for a list).
- The key move of the solution should be unobvious. Obvious moves such as checks, captures, and (in directmates) moves which restrict the movement of the black king, make for bad keys. Keys which deprive the black king of some squares it could move to (flight squares) but at the same time surrender an equal or greater number of flights are acceptable. Key moves which prevent the enemy from playing a checking move are also undesirable, particularly in cases where there is no mate provided after the checking move.
- Every piece on the board should serve a purpose, either to enable the actual solution, or to exclude alternative solutions. Extra units should not be added to create "red herrings" (this is called dressing the board), except in rare cases where this is part of the theme. If the theme can be shown with fewer total units, it should be.
- The problem should exhibit economy of moves. If the theme can be shown in fewer moves, it should be.
Example problem
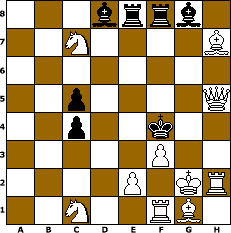 | | White to play and mate in two. |
To the right is a problem composed by T. Taverner in 1881. It is a directmate, with white to move and mate in 2.
The key move is Rh1. This is difficult to find because it makes no threat -- instead, it puts black in zugzwang, a situation where every move is worse than no move, yet the player has to move anyway. Each of black´s nineteen legal replies allows an immediate mate. For example, if black defends with 1...Bxh7, the d5 square is no longer guarded, and white mates with 2.Nd5#. Or if black plays 1...Re5, he blocks that escape square for his king allowing 2.Qg4#. Yet if black could pass (i.e. make no move at all) white would have no way to mate on his second move.
The thematic approach to solving is then to notice that in the original position, black is already almost in zugzwang. If black were compelled to play first, only Re3 and Bg5 would not allow immediate mate. However, each of those two moves blocks a critical escape square for the black king (a flight square), and once white has removed his rook from h2 he can put some other piece on that square to deliver mate: 1...Re3 2. Bh2# and 1...Bg5 2.Qh2#.
The arrangement of the black rooks and bishops, with a pair of adjacent rooks flanked by a pair of bishops, is known to problemists as Organ Pipes. This arrangement means the black pieces get in the way of each other: for example, consider what happens after the key if black plays 1...Bf7. White now mates with 2.Qf5#, a move which is only possible because the bishop black moved has got in the way of the rook´s guard of f5 - this is known as a self-interference. Similarly, if black tries 1...Rf7, this interferes with the bishop´s guard of d5, meaning white can mate with Nd5#. Mutual interferences like this, between two pieces on one square, are known as Grimshaw interferences. There are several Grimshaw interferences in this problem.
Abbreviations
For reasons of space and internationality, various abbreviations are often used in chess problem journals to indicate a problem´s stipulation (whether it is a mate in two, helpmate in four, or whatever). The most common are:
- # - checkmate
- = - stalemate (occasionally p, standing for pat, the French for stalemate, is used instead)
- h - helpmate
- s - selfmate
- r - reflexmate
- ser- - series
These are combined with a number indicating how many moves the target must be achieved in. "#3", therefore, indicates a mate in three, while "ser-h=14" indicates a series-helpstalemate in 14 (Black makes 14 moves in a row, such that White can subsequently make one move to deliver stalemate).
In studies, the symbols + and = are used to indicate "White to play and win" and "White to play and draw" respectively.
Tournaments
Various tournaments (or tourneys) exist for both the composition and solving of chess problems.
Composition tournaments
Composition tourneys may be formal or informal. In formal tourneys the competing problems are not published before they are judged, while in informal tourneys they are. Informal tourneys are often run by problem magazines and other publications with a regular problem section; it is common for every problem to have been published in a particular magazine within a particular year to be eligible for an informal award. Formal tourneys are often held to commemorate a particular event or person. The World Chess Composing Tournament (WCCT) is a formal tourney for national teams organised by the Permanent Commission of the FIDE for Chess Composition (PCCC).
In both formal and informal tourneys, entries will normally be limited to a particular genre of problem (for example, mate in twos, moremovers, helpmates) and may or may not have additional restrictions (for example, problems in patrol chess, problems showing the Lacny theme, problems using fewer than nine units). Honours are usually awarded in three grades: these are, in descending order of merit, prizes, honourable mentions and commendations. As many problems as the judge sees fit may be placed in each grade, and the problems within each grade may or may not be ranked (so an award may include a 1st Honourable Mention, a 2nd Honourable Mention and a 3rd Honourable Mention, or just three unranked Honourable Mentions).
After an award is published, there is a period (typically around three months) in which individuals may claim honoured problems are anticipated (that an identical problem has been published at an earlier date) or unsound (that a problem has cooks or no solution). If such claims are upheld, the award may be adjusted accordingly. At the end of this period, the award becomes final. It is normal to indicate any honour a problem has received when it is republished.
Solving tournaments
Solving tournaments also fall into two main types. In tourneys conducted by correspondence, the participants send their entries by post or email. These are often run on similar terms to informal composition tourneys; indeed, the same problems which are entries in the informal composition tourney are often also set in the solving tourney. It is impossible to eliminate the use of computers in such tournaments, though some problems, such as those with particularly long solutions, will not be well-suited to solution by computer.
Other solving tourneys are held with all participants present at a particular time and place. They have only a limited amount of time to solve the problems, and the use of any solving aid other than a chess set is prohibited. The most notable tournament of this type is the World Chess Solving Championship, organised by the PCCC.
In types of tourney, each problem is worth a specified number of points, often with bonus points for finding cooks or correctly claiming no solution. Incomplete solutions are awarded an appropriate proportion of the points available. The solver amassing the most points is the winner.
Titles
Just as in over-the-board play, the titles International Grandmaster, International Master and FIDE Master are awarded by FIDE via the Permanent Commission of the FIDE for Chess Composition (PCCC) for especially distinguished problem and study composers and solvers (unlike over-the-board chess, however, there are no women-only equivalents to these titles in problem chess).
For composition, the International Master title was established in 1959, with Andre Cheron, Arnolodo Ellerman, Alexander Gerbstmann, Jan Hartong and Cyril Kipping being the first honorary reciepients. In subsequent years, qualification for the IM title, as well as for the GM title (first awarded in 1972 to Genrikh Kasparyan, Lev Loshinsky, Comins Mansfield and Eeltje Visserman) and the FM title (first awarded 1990) has been determined on the basis of the number of problems or studies a composer had selected for publication in the FIDE Albums. These are collections of the best problems and studies composed in a particular three year period, as selected by FIDE-appointed judges. Each problem published in an album is worth one point; each study is worth 1 2/3; joint compositions are worth the same divided by the number of composers. For the FIDE Master title, a composer must accumulate 12 points; for the International Master title, 25 points are needed; and for the Grandmaster title, a composer must have 70 points.
For solvers, the GM and IM titles were both first awarded in 1982; the FM title followed in 1997. GM and IM titles can only be gained by participating in the official World Chess Solving Championship (WCSC): to become a GM, a solver must score at least 90% of the winner´s points and on each occasion finish in at least tenth place three times within ten successive WCSCs. For the IM title they must score at least 80% of the winner´s points and each time finish in at least fifteenth place twice within five successive WCSCs; alternatively, winning a single WCSC or scoring as many points as the winner in a single WCSC will earn the IM title. For the FM title, the solver must score at least 75% of the winners points and each time finish within the top 40% of participants in any two PCCC-approved solving competitions.
The title International Judge of Chess Compositions is given to individuals considered capable of judging compositing tourneys at the highest level.
Further reading
- Andrei Frolkin and Gerd Wilts, Shortest Proof Games (1991) - a collection of 170 proof games (published in Germany, but in English)
- Michael Lipton, R. C. O. Matthews and John Rice, Chess Problems: Introduction to an Art (Faber, 1963)
- Jeremy Morse, Chess Problems: Tasks and Records (Faber and Faber, 1995, revised edition 2001) - concentrates on maximum tasks and records
- John Nunn, Solving in Style (1985) - problems seen from the point of view of the solver
- John Rice, Chess Wizardry: The New ABC of Chess Problems (Batsford, 1996) - a general overview of chess problems, including an extensive A-Z of themes and terms, and 460 problems. Widely regarded as the best single-volume work in English on the subject.
- Kenneth S. Howard, How To Solve Chess Problems (Dover, 1961) - A preliminary section of 30 pages is a useful introduction for novice solvers; then 112 problems with discussion
|
